One of the most significant advances going from TPM1.2 to TPM2 was the addition of algorithm agility: The ability of TPM2 to work with arbitrary symmetric and asymmetric encryption schemes. In practice, in spite of this much vaunted agile encryption capability, most actual TPM2 chips I’ve seen only support a small number of asymmetric encryption schemes, usually RSA2048 and a couple of Elliptic Curves. However, the ability to support any Elliptic Curve at all is a step up from TPM1.2. This blog post will detail how elliptic curve schemes can be integrated into existing cryptographic systems using TPM2. However, before we start on the practice, we need at least a tiny swing through the theory of Elliptic Curves.
What is an Elliptic Curve?
An Elliptic Curve (EC) is simply the set of points that lie on the curve in the two dimensional plane (x,y) defined by the equation
y2 = x3 + ax + b
which means that every elliptic curve can be parametrised by two constants a and b. The set of all points lying on the curve plus a point at infinity is combined with an addition operation to produce an abelian (commutative) group. The addition property is defined by drawing straight lines between two points and seeing where they intersect the curve (or picking the infinity point if they don’t intersect). Wikipedia has a nice diagrammatic description of this here. The infinity point acts as the identity of the addition rule and the whole group is denoted E.
The utility for cryptography is that you can define an integer multiplier operation which is simply the element added to itself n times, so for P ∈ E, you can always find Q ∈ E such that
Q = P + P + P … = n × P
And, since it’s a simple multiplication like operation, it’s very easy to compute Q. However, given P and Q it is computationally very difficult to get back to n. In fact, it can be demonstrated mathematically that trying to compute n is equivalent to the discrete logarithm problem which is the mathematical basis for the cryptographic security of RSA. This also means that EC keys suffer the same (actually more so) problems as RSA keys: they’re not Quantum Computing secure (vulnerable to the Quantum Shor’s algorithm) and they would be instantly compromised if the discrete logarithm problem were ever solved.
Therefore, for any elliptic curve, E, you can choose a known point G ∈ E, select a large integer d and you can compute a point P = d × G. You can then publish (P, G, E) as your public key knowing it’s computationally infeasible for anyone to derive your private key d.
For instance, Diffie-Hellman key exchange can be done by agreeing (E, G) and getting Alice and Bob to select private keys dA, dB. Then knowing Bob’s public key PB, Alice can select a random integer r, which she publishes, and compute a key agreement as a secret point on the Elliptic Curve (r dA) × PB. Bob can derive the same Elliptic Curve point because
(r dA) × PB = (r dA)dB × G = (r dB) dA × G = (r dB) × PA
The agreement is a point on the curve, but you can use an agreed hashing or other mechanism to get from the point to a symmetric key.
Seems simple, but the problem for computing is that we really want to use integers and right at the moment the elliptic curve is defined over all the real numbers, meaning E is of infinite size and involves floating point computations (of rather large precision).
Elliptic Curves over Finite Fields
Fortunately there is a mathematical theory of finite fields, called Galois Theory, which allows us to take the Galois Field over prime number p, which is denoted GF(p), and compute Elliptic Curve points over this field. This derivation, which is mathematically rather complicated, is denoted E(GF(p)), where every point (x,y) is represented by a pair of integers between 0 and p-1. There is another theory that says the number of elements in E(GF(p))
n = |E(GF(p))|
is roughly the same size as p, meaning if you choose a 32 bit prime p, you likely have a field over roughly 2^32 elements. For every point P in E(GF(p)) it is also mathematically proveable that n × P = 0. where 0 is the zero point (which was the infinity point in the real elliptic curve).
This means that you can take any point, G, in E(GF(p)) and compute a subgroup based on it:
EG = { ∀m ∈ Zn : m × G }
If you’re lucky |EG| = |E(GF(p))| and G is the generator of the entire group. However, G may only generate a subgroup and you will find |EG| = h|E(GF(p))| where integer h is called the cofactor. In general you want the cofactor to be small (preferably less than four) for EG to be cryptographically useful.
For a computer’s purposes, EG is the elliptic curve group used for integer arithmetic in the cryptographic algorithms. The Curve and Generator is then defined by (p, a, b, Gx, Gy, n, h) which are the published parameters of the key (Gx, Gy represent the x and y elements of point G). You select a random number d as your private key and your public key P = d × G exactly as above, except now P is easy to compute with integer operations.
Problems with Elliptic Curves
Although I stated above that solving P = d × G is equivalent in difficulty to the discrete logarithm problem, that’s not generally true. If the discrete logarithm problem were solved, then we’d easily be able to compute d for every generator and curve, but it is possible to pick curves for which d can be easily computed without solving the discrete logarithm problem. This is the reason why you should never pick your own curve parameters (even if you think you know what you’re doing) because it’s very easy to choose a compromised curve. As a demonstration of the difficulty of the problem: each of the major nation state actors, Russia, China and the US, publishes their own curve parameters for use in their own cryptographic EC implementations and each of them thinks the parameters published by the others is compromised in a way that allows the respective national security agencies to derive private keys. So if nation state actors can’t tell if a curve is compromised or not, you surely won’t be able to either.
Therefore, to be secure in EC cryptography, you pick and existing curve which has been vetted and select some random Generator Point on it. Of course, if you’re paranoid, that means you won’t be using any of the nation state supplied curves …
Using the TPM2 with Elliptic Curves in Cryptosystems
The initial target for this work was the openssl cryptosystem whose libraries are widely used for deriving other uses (like https in apache or openssh). Originally, when I did the initial TPM2 enabling of openssl as described in this blog post, I added TPM2 as a patch to the existing TPM 1.2 openssl_tpm_engine. Unfortunately, openssl_tpm_engine seems to be pretty much defunct at this point, so I started my own openssl_tpm2_engine as a separate git tree to begin experimenting with Elliptic Curve keys (if you don’t use git, you can download the tar file here). One of the benefits to running my own source tree is that I can now add a testing infrastructure that makes use of the IBM TPM emulator to make sure that the basic cryptographic operations all work which means that make check functions even when a TPM2 isn’t available. The current key creation and import algorithms use secured connections to the TPM (to avoid eavesdropping) which means it’s only really possible to construct them using the IBM TSS. To make all of this easier, I’ve set up an openSUSE Build Service repository which is building for all major architectures and the openSUSE and Fedora distributions (ignore the failures, they’re currently induced because the TPM emulator only currently works on 64 bit little endian systems, so make check is failing, but the TPM people at IBM are working on this, so eventually the builds should be complete).
TPM2 itself also has some annoying restrictions. The biggest of which is that it doesn’t allow you to pass in arbitrary elliptic curve parameters; you may only use elliptic curves which the TPM itself knows. This will be annoying if you have an existing EC key you’re trying to import because the TPM may reject it as an unknown algorithm. For instance, openssl can actually compute with arbitrary EC parameters, but has 39 current elliptic curves parametrised by name. By contrast, my Nuvoton TPM2 inside my Dell XPS 13 knows precisely two curves:
jejb@jarvis:~> create_tpm2_key --list-curves
prime256v1
bnp256
However, assuming you’ve picked a compatible curve for your EC private key (and you’ve defined a parent key for the storage hierarchy) you can simply import it to a TPM bound key:
create_tpm2_key -p 81000001 -w key.priv key.tpm
The tool will report an error if it can’t convert the curve parameters to a named elliptic curve known to the TPM
jejb@jarvis:~> openssl genpkey -algorithm EC -pkeyopt ec_paramgen_curve:brainpoolP256r1 > key.priv
jejb@jarvis:~> create_tpm2_key -p 81000001 -w key.priv key.tpm
TPM does not support the curve in this EC key
openssl_to_tpm_public failed with 166
TPM_RC_CURVE - curve not supported Handle number unspecified
You can also create TPM resident private keys simply by specifying the algorithm
create_tpm2_key -p 81000001 --ecc bnp256 key.tpm
Once you have your TPM based EC keys, you can use them to create public keys and certificates. For instance, you create a self-signed X509 certificate based on the tpm key by
openssl req -new -x509 -sha256 -key key.tpm -engine tpm2 -keyform engine -out my.crt
Why you should use EC keys with the TPM
The initial attraction is the same as for RSA keys: making it impossible to extract your private key from the system. However, the mathematical calculations for EC keys are much simpler than for RSA keys and don’t involve finding strong primes, so it’s much simpler for the TPM (being a fairly weak calculation machine) to derive private and public EC keys. For instance the times taken to derive a RSA key from the primary seed and an EC key differ dramatically
jejb@jarvis:~> time tsscreateprimary -hi o -ecc bnp256 -st
Handle 80ffffff
real 0m0.111s
user 0m0.000s
sys 0m0.014s
jejb@jarvis:~> time tsscreateprimary -hi o -rsa -st
Handle 80ffffff
real 0m20.473s
user 0m0.015s
sys 0m0.084s
so for a slow system like the TPM, using EC keys is a significant speed advantage. Additionally, there are other advantages. The standard EC Key signature algorithm is a modification of the NIST Digital Signature Algorithm called ECDSA. However DSA and ECDSA require a cryptographically strong (and secret) random number as Sony found out to their cost in the EC Key compromise of Playstation 3. The TPM is a good source of cryptographically strong random numbers and if it generates the signature internally, you can be absolutely sure of keeping the input random number secret.
Why you might want to avoid EC keys altogether
In spite of the many advantages described above, EC keys suffer one additional disadvantage over RSA keys in that Elliptic Curves in general are very hot fields of mathematical research so even if the curve you use today is genuinely not compromised, it’s not impossible that a mathematical advance tomorrow will make the curve you chose (and thus all the private keys you generated) vulnerable. Of course, the same goes for RSA if anyone ever cracks the discrete logarithm problem, but solving that problem would likely be fully published to world acclaim and recognition as a significant contribution to the advancement of number theory. Discovering an attack on a currently used elliptic curve on the other hand might be better remunerated by offering to sell it privately to one of the national security agencies …
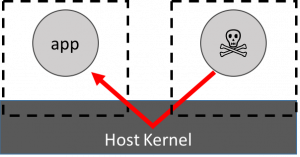 The HAP attack worry with standard containers is shown on the left: that a malicious application can breach the containment wall and attack an innocent application. This attack is thought to be facilitated by the breadth of the syscall interface in standard containers so the guiding star in developing Nabla Containers was a methodology for measuring the reduction in the HAP (and hence the improvement in containment), but the initial impetus came from the observation that unikernel systems are nicely modular in the libOS approach, can be used to emulate systemcalls and, thanks to rumprun, have a wide set of support for modern web friendly languages (like python, node.js and go) with a fairly thin glue layer. Additionally they have a fairly narrow set of hypercalls that are actually used in practice (meaning they can be made more secure than conventional hypervisors). Code coverage measurements of standard unikernel based kvm images confirmed that they did indeed use a far narrower interface.
The HAP attack worry with standard containers is shown on the left: that a malicious application can breach the containment wall and attack an innocent application. This attack is thought to be facilitated by the breadth of the syscall interface in standard containers so the guiding star in developing Nabla Containers was a methodology for measuring the reduction in the HAP (and hence the improvement in containment), but the initial impetus came from the observation that unikernel systems are nicely modular in the libOS approach, can be used to emulate systemcalls and, thanks to rumprun, have a wide set of support for modern web friendly languages (like python, node.js and go) with a fairly thin glue layer. Additionally they have a fairly narrow set of hypercalls that are actually used in practice (meaning they can be made more secure than conventional hypervisors). Code coverage measurements of standard unikernel based kvm images confirmed that they did indeed use a far narrower interface.